Describe in Your Own Words the Central Limit Theorem
Experts are tested by Chegg as specialists in their subject area. The theorem states that if we add identically distributed independent random variables their normalized sum will tend towards a normal distribution.
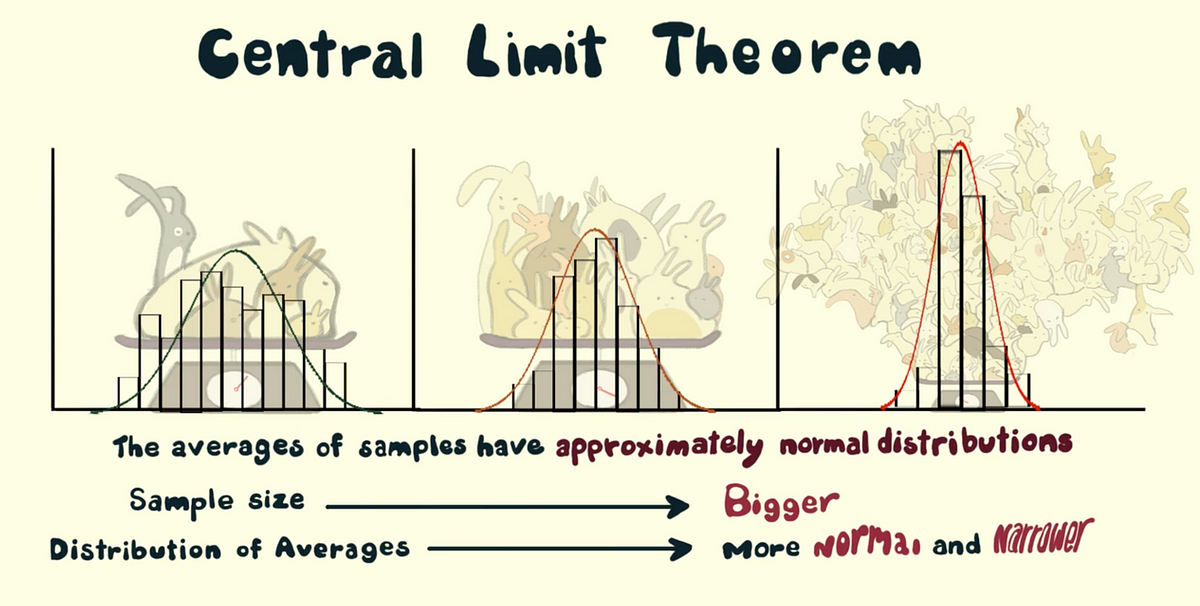
Central Limit Theorem In Action And Examples From Its Practical By Ceren Iyim Towards Data Science
Lets see this through a simple example.

. The meaning of CENTRAL LIMIT THEOREM is any of several fundamental theorems of probability and statistics that state the conditions under which the distribution of a sum of independent random variables is approximated by the normal distribution. The Central Limit Theorem CLT for short basically says that for non-normal data the distribution of the sample means has an approximate normal distribution no matter what the distribution of the original data looks like as long as the sample size is large enough usually at least 30 and all samples have the same size. The Central Limit Theorem CLT is a statistical concept that states that the sample mean distribution of a random variable will assume a near-normal or normal distribution if the sample size is large enough.
In my own words the Central Limit Theorem explains how the sum or average of a set of variables or answers tends to a certain distribution. The Central Limit Theorem in probability theory a theorem that establishes the normal distribution as the distribution to which the mean average of almost any set of independent and randomly generated variables rapidly converges. We investigated the probability distribution sampling.
It also provides us with the mean and standard deviation of this distribution. The Central Limit Theorem CLT is one of the most popular theorems in statistics and its very useful in real world problems. According to the Central Limit Theorem the arithmetic mean of a sufficiently large number of iterates of independent random variables at a given condition is normally distributed.
The central limit theorem CLT states that the distribution of sample means approximates a normal distribution as the sample size gets larger regardless of. The conditions that must be met are that np 5 and n 1-p 5. The central limit theorem explains why the normal distribution arises so commonly and why it is.
Describe it in your own words. Once we take repeated samples from some kind of particular group the central limit theorem shows us precisely whatever the form including its distribution implies. The Central Limit Theorem widely regarded as the crown jewel of probability and statistics is the most beautiful and important in probability theory.
We review their content and use your feedback to keep the quality high. To keep the data from changing select the random numbers you. The central limit theorem also tells us that no matter what the distribution of the population is the shape of the sampling distribution will approach normality as the sample size N increases.
B No - route B journey times are normally distributed. A No - route A journey times are normally distributed. The central limit theorem CLT is a statistical theory that states that given a sufficiently large sample size from a population with a finite level of variance the mean of all samples from the same population will be approximately.
The central limit theorem allows us to use a normal distribution for some very meaningful and important applications. Indicate where if anywhere in this question you needed to make use of the Central Limit Theorem. 1 Describe the Central Limit Theorem in your own words.
Up to 25 cash back The central limit theorem allows us to approximate the binomial distribution in this way. The central limit theorem concerns the sampling distribution of the sample means. The Central Limit Theorem provides more than the proof that the sampling distribution of means is normally distributed.
In simple terms the theorem states that the sampling distribution of the mean. For those new to statistics this definition may seem a bit intimidating. Typically these are met through having a large sample.
In this article well see why the Central Limit Theorem is so useful and how to apply it. The theorem states that if we add identically. In a lot of situations where you use statistics the ultimate goal is to identify the characteristics of a population.
Mean Mean is an essential concept in mathematics and statistics. Further as discussed above the expected value of the mean μ x μ x is equal to the mean of the population of the original data which is what we are interested in estimating. The Central Limit Theorem which is widely regarded as the crown jewel of probability and statistics is the most beautiful and important theorem in probability theory.
2 UseRANDBETWEEN 1 100 to create 250 samples of size n 30 each by generating random integer whole numbers between 1 and 100. Why is it so important in statistical analysis. One which is much applied in sampling and which states that the distribution of a mean of a sample from a.
This is important in daily life because I could for example post a homework question on Quora asking how to explain CLT in my own words and then if I receive enough answers I could submit the average answer I receive such as this. Accurately the distributions of means determined via repeated measurements can reach normality as when the small samples get bigger. This is an experiment to illustrate the Central Limit Theorem.
The theorem states that if we add identically distributed independent random variables then their normalized sum will tend towards a normal distribution. D Yes - Car journey times are from an unknown distribution. The central limit theorem says that this sampling distribution is approximately normalcommonly known as a bell curve.
Lets investigate the central limit theorem CLT. This approximation improves as we increase the size of the simple random samples that are used. The central limit theorem states that whenever a random sample of size n is taken from any distribution with mean and variance then the sample mean will be approximately normally distributed with mean and variance.
The Central Limit Theorm. We may ask about the overall shape of the sampling distribution. The larger the value of the sample size the better the approximation to the normal.
View the full answer. Who are the experts. The central limit theorem CLT states that the means of random samples drawn from any distribution with mean m and variance s2 will have an approximately normal distribution with a mean equal to m and a variance equal to s2 n.
The central limit theorem is perhaps the most fundamental result in all of statistics. It allows us to understand the behavior of estimates across repeated sampling and thereby conclude if a result from a given sample can be declared to be statistically significant that is different from some null hypothesized value. Central Limit Theorem Statement.
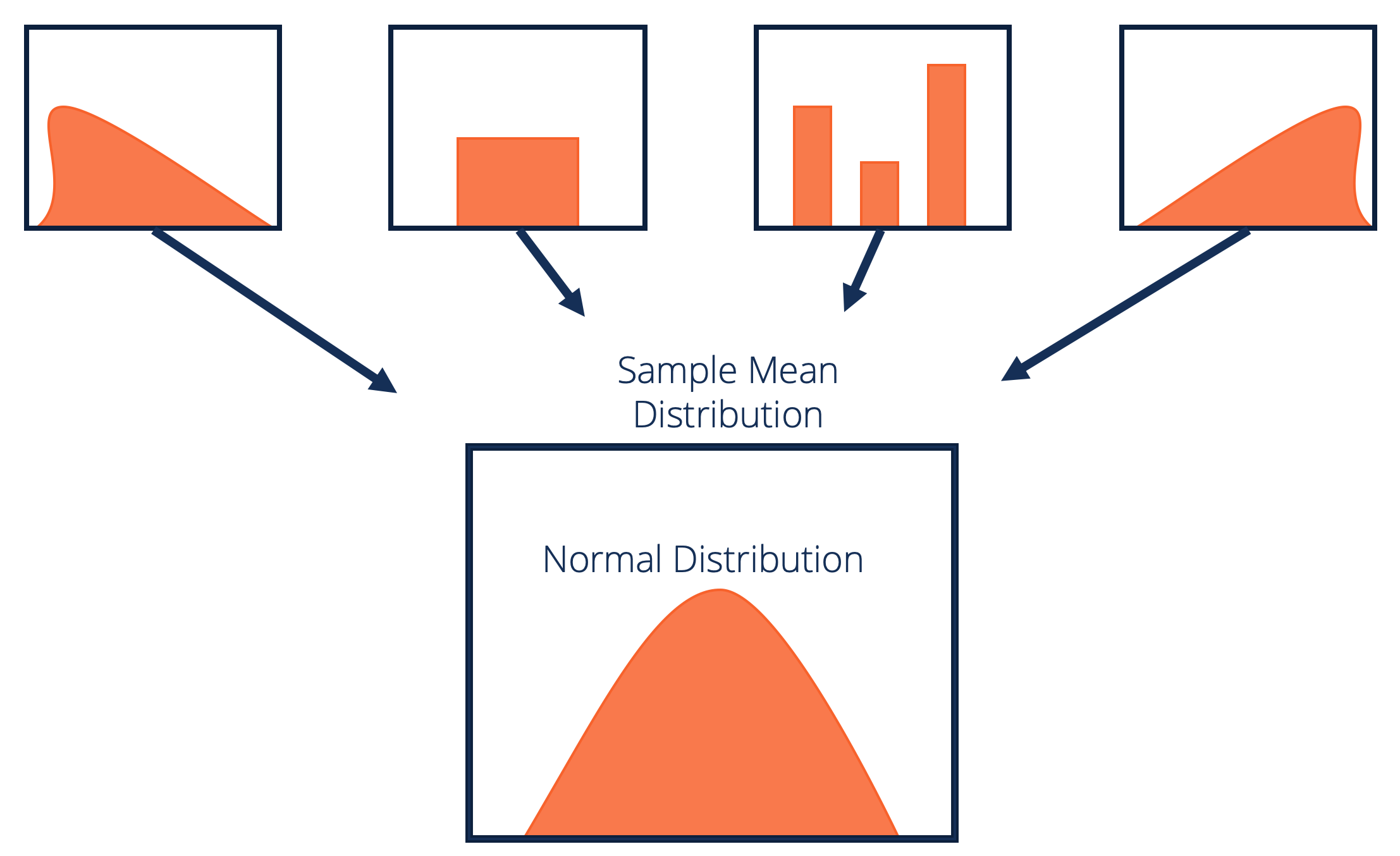
Central Limit Theorem Overview History And Example

Central Limit Theorem Simplified By Seema Singh Medium
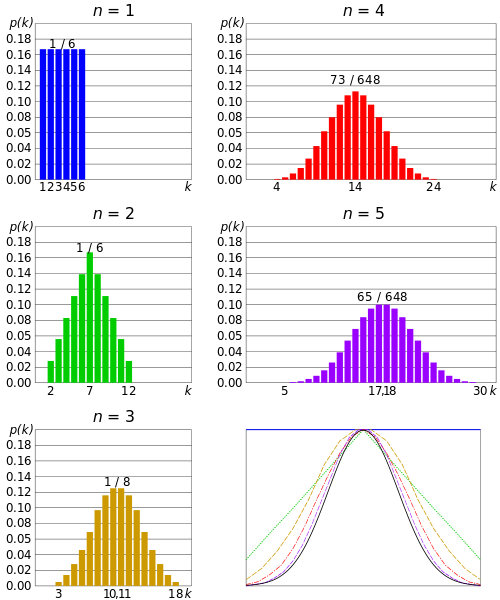
Central Limit Theorem Definition And Examples Statistics How To
No comments for "Describe in Your Own Words the Central Limit Theorem"
Post a Comment